Working with Graphs
In Akka Streams computation graphs are not expressed using a fluent DSL like linear computations are, instead they are written in a more graph-resembling DSL which aims to make translating graph drawings (e.g. from notes taken from design discussions, or illustrations in protocol specifications) to and from code simpler. In this section we’ll dive into the multiple ways of constructing and re-using graphs, as well as explain common pitfalls and how to avoid them.
Graphs are needed whenever you want to perform any kind of fan-in ("multiple inputs") or fan-out ("multiple outputs") operations.
Considering linear Flows to be like roads, we can picture graph operations as junctions: multiple flows being connected at a single point.
Some graph operations which are common enough and fit the linear style of Flows, such as Concat (which concatenates two
streams, such that the second one is consumed after the first one has completed), may have shorthand methods defined on
Flow or Source themselves, however you should keep in mind that those are also implemented as graph junctions.
Constructing Graphs
Graphs are built from simple Flows which serve as the linear connections within the graphs as well as junctions which serve as fan-in and fan-out points for Flows. Thanks to the junctions having meaningful types based on their behavior and making them explicit elements these elements should be rather straightforward to use.
Akka Streams currently provide these junctions (for a detailed list see Overview of built-in stages and their semantics):
- Fan-out
Broadcast<T>– (1 input, N outputs) given an input element emits to each outputBalance<T>– (1 input, N outputs) given an input element emits to one of its output portsUnzipWith<In,A,B,...>– (1 input, N outputs) takes a function of 1 input that given a value for each input emits N output elements (where N <= 20)UnZip<A,B>– (1 input, 2 outputs) splits a stream of(A,B)tuples into two streams, one of typeAand one of typeB
- Fan-in
Merge<In>– (N inputs , 1 output) picks randomly from inputs pushing them one by one to its outputMergePreferred<In>– likeMergebut if elements are available onpreferredport, it picks from it, otherwise randomly fromothersMergePrioritized<In>– likeMergebut if elements are available on all input ports, it picks from them randomly based on theirpriorityZipWith<A,B,...,Out>– (N inputs, 1 output) which takes a function of N inputs that given a value for each input emits 1 output elementZip<A,B>– (2 inputs, 1 output) is aZipWithspecialized to zipping input streams ofAandBinto an(A,B)tuple streamConcat<A>– (2 inputs, 1 output) concatenates two streams (first consume one, then the second one)
One of the goals of the GraphDSL DSL is to look similar to how one would draw a graph on a whiteboard, so that it is simple to translate a design from whiteboard to code and be able to relate those two. Let's illustrate this by translating the below hand drawn graph into Akka Streams:
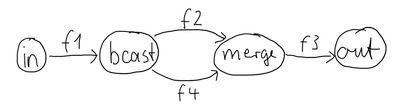
Such graph is simple to translate to the Graph DSL since each linear element corresponds to a Flow,
and each circle corresponds to either a Junction or a Source or Sink if it is beginning
or ending a Flow. Junctions must always be created with defined type parameters.
var g = RunnableGraph.FromGraph(GraphDsl.Create(builder =>
{
var source = Source.From(Enumerable.Range(1, 10));
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
var broadcast = builder.Add(new Broadcast<int>(2));
var merge = builder.Add(new Merge<int>(2));
var f1 = Flow.Create<int>().Select(x => x + 10);
var f2 = Flow.Create<int>().Select(x => x + 10);
var f3 = Flow.Create<int>().Select(x => x + 10);
var f4 = Flow.Create<int>().Select(x => x + 10);
builder.From(source).Via(f1).Via(broadcast).Via(f2).Via(merge).Via(f3).To(sink);
builder.From(broadcast).Via(f4).To(merge);
return ClosedShape.Instance;
}));
Note
Junction reference equality defines graph node equality (i.e. the same merge instance used in a GraphDSL refers to the same location in the resulting graph).
By looking at the snippets above, it should be apparent that the GraphDSL.Builder object is mutable.
The reason for this design choice is to enable simpler creation of complex graphs, which may even contain cycles.
Once the GraphDSL has been constructed though, the GraphDSL instance is immutable, thread-safe, and freely shareable.
The same is true of all graph pieces—sources, sinks, and flows—once they are constructed.
This means that you can safely re-use one given Flow or junction in multiple places in a processing graph.
We have seen examples of such re-use already above: the merge and broadcast junctions were imported
into the graph using builder.Add(...), an operation that will make a copy of the blueprint that
is passed to it and return the inlets and outlets of the resulting copy so that they can be wired up.
Another alternative is to pass existing graphs—of any shape—into the factory method that produces a
new graph. The difference between these approaches is that importing using builder.Add(...) ignores the
materialized value of the imported graph while importing via the factory method allows its inclusion;
for more details see Stream Materialization.
In the example below we prepare a graph that consists of two parallel streams,
in which we re-use the same instance of Flow, yet it will properly be
materialized as two connections between the corresponding Sources and Sinks:
var topHeadSink = Sink.First<int>();
var bottomHeadSink = Sink.First<int>();
var sharedDoubler = Flow.Create<int>().Select(x => x*2);
RunnableGraph.FromGraph(GraphDsl.Create(topHeadSink, bottomHeadSink, Keep.Both,
(builder, topHs, bottomHs) =>
{
var broadcast = builder.Add(new Broadcast<int>(2));
var source = Source.Single(1).MapMaterializedValue<Tuple<Task<int>, Task<int>>>(_ => null);
builder.From(source).To(broadcast.In);
builder.From(broadcast.Out(0)).Via(sharedDoubler).To(topHs.Inlet);
builder.From(broadcast.Out(1)).Via(sharedDoubler).To(bottomHs.Inlet);
return ClosedShape.Instance;
}));
Constructing and Combining Partial Graphs
Sometimes it is not possible (or needed) to construct the entire computation graph in one place, but instead construct all of its different phases in different places and in the end connect them all into a complete graph and run it.
This can be achieved by returning a different Shape than ClosedShape, for example FlowShape(in, out), from the
function given to GraphDSL.Create. See Predefined shapes for a list of such predefined shapes.
Making a Graph a RunnableGraph requires all ports to be connected, and if they are not
it will throw an exception at construction time, which helps to avoid simple
wiring errors while working with graphs. A partial graph however allows
you to return the set of yet to be connected ports from the code block that
performs the internal wiring.
Let's imagine we want to provide users with a specialized element that given 3 inputs will pick the greatest int value of each zipped triple. We'll want to expose 3 input ports (unconnected sources) and one output port (unconnected sink).
var pickMaxOfThree = GraphDsl.Create(b =>
{
var zip1 = b.Add(ZipWith.Apply<int, int, int>(Math.Max));
var zip2 = b.Add(ZipWith.Apply<int, int, int>(Math.Max));
b.From(zip1.Out).To(zip2.In0);
return new UniformFanInShape<int, int>(zip2.Out, zip1.In0, zip1.In1, zip2.In1);
});
var resultSink = Sink.First<int>();
var g = RunnableGraph.FromGraph(GraphDsl.Create(resultSink, (b, sink) =>
{
// importing the partial graph will return its shape (inlets & outlets)
var pm3 = b.Add(pickMaxOfThree);
var s1 = Source.Single(1).MapMaterializedValue<Task<int>>(_ => null);
var s2 = Source.Single(2).MapMaterializedValue<Task<int>>(_ => null);
var s3 = Source.Single(3).MapMaterializedValue<Task<int>>(_ => null);
b.From(s1).To(pm3.In(0));
b.From(s2).To(pm3.In(1));
b.From(s3).To(pm3.In(2));
b.From(pm3.Out).To(sink.Inlet);
return ClosedShape.Instance;
}));
var max = g.Run(materializer);
max.Wait(TimeSpan.FromSeconds(3)).Should().BeTrue();
max.Result.Should().Be(3);
As you can see, first we construct the partial graph that contains all the zipping and comparing of stream
elements. This partial graph will have three inputs and one output, wherefore we use the UniformFanInShape.
Then we import it (all of its nodes and connections) explicitly into the closed graph built in the second step in which all the undefined elements are rewired to real sources and sinks. The graph can then be run and yields the expected result.
Warning
Please note that GraphDSL is not able to provide compile time type-safety about whether or not all elements have been properly connected—this validation is performed as a runtime check during the graph's instantiation. A partial graph also verifies that all ports are either connected or part of the returned Shape.
Constructing Sources, Sinks and Flows From Partial Graphs
Instead of treating a partial graph as simply a collection of flows and junctions which may not yet all be
connected it is sometimes useful to expose such a complex graph as a simpler structure,
such as a Source, Sink or Flow.
In fact, these concepts can be easily expressed as special cases of a partially connected graph:
Sourceis a partial graph with exactly one output, that is it returns aSourceShape.Sinkis a partial graph with exactly one input, that is it returns aSinkShape.Flowis a partial graph with exactly one input and exactly one output, that is it returns aFlowShape.
Being able to hide complex graphs inside of simple elements such as Sink / Source / Flow enables you to easily create one complex element and from there on treat it as simple compound stage for linear computations.
In order to create a Source from a graph the method Source.fromGraph is used, to use it we must have a
IGraph<SourceShape, T>. This is constructed using GraphDSL.Create and returning a SourceShape
from the function passed in . The single outlet must be provided to the SourceShape.Of method and will become "the sink that must be attached before this Source can run".
Refer to the example below, in which we create a Source that zips together two numbers, to see this graph construction in action:
var pairs = Source.FromGraph(GraphDsl.Create(b =>
{
// prepare graph elements
var zip = b.Add(new Zip<int, int>());
Func<Source<int, Task<Tuple<int, int>>>> ints = () =>
Source.From(Enumerable.Range(1, int.MaxValue))
.MapMaterializedValue<Task<Tuple<int, int>>>(_ => null);
// connect the graph
b.From(ints().Where(x => x%2 != 0)).To(zip.In0);
b.From(ints().Where(x => x % 2 == 0)).To(zip.In1);
// expose port
return new SourceShape<Tuple<int, int>>(zip.Out);
}));
var firstPair = pairs.RunWith(Sink.First<Tuple<int, int>>(), materializer);
Similarly the same can be done for a Sink<T>, using SinkShape.Of in which case the provided value
must be an Inlet<T>. For defining a Flow<T> we need to expose both an inlet and an outlet:
var pairUpWithToString = Flow.FromGraph(
GraphDsl.Create(b =>
{
// prepare graph elements
var broadcast = b.Add(new Broadcast<int>(2));
var zip = b.Add(new Zip<int, string>());
// connect the graph
b.From(broadcast.Out(0)).Via(Flow.Create<int>().Select(x => x)).To(zip.In0);
b.From(broadcast.Out(1)).Via(Flow.Create<int>().Select(x => x.ToString())).To(zip.In1);
// expose ports
return new FlowShape<int, Tuple<int, string>>(broadcast.In, zip.Out);
}));
pairUpWithToString.RunWith(Source.From(new[] {1}), Sink.First<Tuple<int, string>>(), materializer);
Combining Sources and Sinks with Simplified API
There is a simplified API you can use to combine sources and sinks with junctions like: Broadcast<T>, Balance<T>, Merge<In> and Concat<A> without the need for using the Graph DSL. The combine method takes care of constructing the necessary graph underneath. In following example we combine two sources into one (fan-in):
var sourceOne = Source.Single(1);
var sourceTwo = Source.Single(2);
var merged = Source.Combine(sourceOne, sourceTwo, i => new Merge<int, int>(i));
var mergedResult = merged.RunWith(Sink.Aggregate<int, int>(0, (agg, i) => agg + i), materializer);
The same can be done for a Sink<T> but in this case it will be fan-out:
var sendRemotely = Sink.ActorRef<int>(actorRef, "Done");
var localProcessing = Sink.ForEach<int>(_ => { /* do something usefull */ })
.MapMaterializedValue(_=> NotUsed.Instance);
var sink = Sink.Combine(i => new Broadcast<int>(i), sendRemotely, localProcessing);
Source.From(new[] {0, 1, 2}).RunWith(sink, materializer);
Building Reusable Graph Components
It is possible to build reusable, encapsulated components of arbitrary input and output ports using the graph DSL.
As an example, we will build a graph junction that represents a pool of workers, where a worker is expressed
as a Flow<I,O,_>, i.e. a simple transformation of jobs of type I to results of type O (as you have seen
already, this flow can actually contain a complex graph inside). Our reusable worker pool junction will
not preserve the order of the incoming jobs (they are assumed to have a proper ID field) and it will use a Balance junction to schedule jobs to available workers. On top of this, our junction will feature a "fast lane", a dedicated port where jobs of higher priority can be sent.
Altogether, our junction will have two input ports of type I (for the normal and priority jobs) and an output port of type O. To represent this interface, we need to define a custom Shape. The following lines show how to do that.
public class PriorityWorkerPoolShape<TIn, TOut> : Shape
{
public PriorityWorkerPoolShape(Inlet<TIn> jobsIn, Inlet<TIn> priorityJobsIn, Outlet<TOut> resultsOut)
{
JobsIn = jobsIn;
PriorityJobsIn = priorityJobsIn;
ResultsOut = resultsOut;
Inlets = ImmutableArray.Create<Inlet>(jobsIn, priorityJobsIn);
Outlets = ImmutableArray.Create<Outlet>(resultsOut);
}
public override ImmutableArray<Inlet> Inlets { get; }
public override ImmutableArray<Outlet> Outlets { get; }
public Inlet<TIn> JobsIn { get; }
public Inlet<TIn> PriorityJobsIn { get; }
public Outlet<TOut> ResultsOut { get; }
public override Shape DeepCopy()
{
return new PriorityWorkerPoolShape<TIn, TOut>((Inlet<TIn>)JobsIn.CarbonCopy(),
(Inlet<TIn>)PriorityJobsIn.CarbonCopy(), (Outlet<TOut>)ResultsOut.CarbonCopy());
}
public override Shape CopyFromPorts(ImmutableArray<Inlet> inlets, ImmutableArray<Outlet> outlets)
{
if (inlets.Length != Inlets.Length)
throw new ArgumentException(
$"Inlets have the wrong length, expected {Inlets.Length} found {inlets.Length}", nameof(inlets));
if (outlets.Length != Outlets.Length)
throw new ArgumentException(
$"Outlets have the wrong length, expected {Outlets.Length} found {outlets.Length}", nameof(outlets));
// This is why order matters when overriding inlets and outlets.
return new PriorityWorkerPoolShape<TIn, TOut>((Inlet<TIn>)inlets[0], (Inlet<TIn>)inlets[1],
(Outlet<TOut>)outlets[0]);
}
}
Predefined Shapes
In general a custom Shape needs to be able to provide all its input and output ports, be able to copy itself, and also be
able to create a new instance from given ports. There are some predefined shapes provided to avoid unnecessary
boilerplate:
SourceShape,SinkShape,FlowShapefor simpler shapes,UniformFanInShapeandUniformFanOutShapefor junctions with multiple input (or output) ports of the same type,FanInShape1,FanInShape2, ...,FanOutShape1,FanOutShape2, ... for junctions with multiple input (or output) ports of different types.
Since our shape has two input ports and one output port, we can just use the FanInShape DSL to define our custom shape:
public class PriorityWorkerPoolShape2<TIn, TOut> : FanInShape<TOut>
{
public PriorityWorkerPoolShape2(IInit init = null)
: base(init ?? new InitName("PriorityWorkerPool"))
{
}
protected override FanInShape<TOut> Construct(IInit init)
=> new PriorityWorkerPoolShape2<TIn, TOut>(init);
public Inlet<TIn> JobsIn { get; } = new Inlet<TIn>("JobsIn");
public Inlet<TIn> PriorityJobsIn { get; } = new Inlet<TIn>("priorityJobsIn");
// Outlet[Out] with name "out" is automatically created
}
Now that we have a Shape we can wire up a Graph that represents our worker pool. First, we will merge incoming normal and priority jobs using MergePreferred, then we will send the jobs to a Balance junction which will fan-out to a configurable number of workers (flows), finally we merge all these results together and send them out through our only output port. This is expressed by the following code:
public static class PriorityWorkerPool
{
public static IGraph<PriorityWorkerPoolShape<TIn, TOut>, NotUsed> Create<TIn, TOut>(
Flow<TIn, TOut, NotUsed> worker, int workerCount)
{
return GraphDsl.Create(b =>
{
var priorityMerge = b.Add(new MergePreferred<TIn>(1));
var balance = b.Add(new Balance<TIn>(workerCount));
var resultsMerge = b.Add(new Merge<TOut>(workerCount));
// After merging priority and ordinary jobs, we feed them to the balancer
b.From(priorityMerge).To(balance);
// Wire up each of the outputs of the balancer to a worker flow
// then merge them back
for (var i = 0; i < workerCount; i++)
b.From(balance.Out(i)).Via(worker).To(resultsMerge.In(i));
// We now expose the input ports of the priorityMerge and the output
// of the resultsMerge as our PriorityWorkerPool ports
// -- all neatly wrapped in our domain specific Shape
return new PriorityWorkerPoolShape<TIn, TOut>(jobsIn: priorityMerge.In(0),
priorityJobsIn: priorityMerge.Preferred, resultsOut: resultsMerge.Out);
});
}
}
All we need to do now is to use our custom junction in a graph. The following code simulates some simple workers
and jobs using plain strings and prints out the results. Actually we used two instances of our worker pool junction
using Add() twice.
var worker1 = Flow.Create<string>().Select(s => "step 1 " + s);
var worker2 = Flow.Create<string>().Select(s => "step 2 " + s);
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
Func<string, Source<string, NotUsed>> createSource = desc =>
Source.From(Enumerable.Range(1, 100))
.Select(s => desc + s);
var priorityPool1 = b.Add(PriorityWorkerPool.Create(worker1, 4));
var priorityPool2 = b.Add(PriorityWorkerPool.Create(worker2, 2));
b.From(createSource("job: ")).To(priorityPool1.JobsIn);
b.From(createSource("priority job: ")).To(priorityPool1.PriorityJobsIn);
b.From(priorityPool1.ResultsOut).To(priorityPool2.JobsIn);
b.From(createSource("one-step, priority : ")).To(priorityPool2.PriorityJobsIn);
var sink = Sink.ForEach<string>(Console.WriteLine).MapMaterializedValue(_ => NotUsed.Instance);
b.From(priorityPool2.ResultsOut).To(sink);
return ClosedShape.Instance;
})).Run(materializer);
Bidirectional Flows
A graph topology that is often useful is that of two flows going in opposite directions. Take for example a codec stage that serializes outgoing messages and deserializes incoming octet streams. Another such stage could add a framing protocol that attaches a length header to outgoing data and parses incoming frames back into the original octet stream chunks. These two stages are meant to be composed, applying one atop the other as part of a protocol stack. For this purpose exists the special type BidiFlow which is a graph that has exactly two open inlets and two open outlets. The corresponding shape is called BidiShape and is defined like this:
/**
* A bidirectional flow of elements that consequently has two inputs and two
* outputs, arranged like this:
*
*
* +------+
* In1 ~>| |~> Out1
* | bidi |
* Out2 <~| |<~ In2
* +------+
*
*/
public sealed class BidiShape<TIn1, TOut1, TIn2, TOut2> : Shape
{
public BidiShape(Inlet<TIn1> in1, Outlet<TOut1> out1, Inlet<TIn2> in2, Outlet<TOut2> out2)
{
}
// implementation details elided ...
}
A bidirectional flow is defined just like a unidirectional Flow as demonstrated for the codec mentioned above:
public interface IMessage { }
public struct Ping : IMessage
{
public Ping(int id)
{
Id = id;
}
public int Id { get; }
}
public struct Pong : IMessage
{
public Pong(int id)
{
Id = id;
}
public int Id { get; }
}
public static ByteString ToBytes(IMessage message)
{
// implementation details elided ...
}
public static IMessage FromBytes(ByteString bytes)
{
// implementation details elided ...
}
var codecVerbose =
BidiFlow.FromGraph(GraphDsl.Create(b =>
{
// construct and add the top flow, going outbound
var outbound = b.Add(Flow.Create<IMessage>().Select(ToBytes));
// construct and add the bottom flow, going inbound
var inbound = b.Add(Flow.Create<ByteString>().Select(FromBytes));
// fuse them together into a BidiShape
return BidiShape.FromFlows(outbound, inbound);
}));
// this is the same as the above
var codec = BidiFlow.FromFunction<IMessage, ByteString, ByteString, IMessage>(ToBytes, FromBytes);
The first version resembles the partial graph constructor, while for the simple case of a functional 1:1 transformation there is a concise convenience method as shown on the last line. The implementation of the two functions is not difficult either:
public static ByteString ToBytes(IMessage message)
{
var order = ByteOrder.LittleEndian;
var ping = message as Ping;
if (ping != null)
return new ByteStringBuilder().PutByte(1).PutInt(ping.Id, order).Result();
var pong = message as Pong;
if (pong != null)
return new ByteStringBuilder().PutByte(2).PutInt(pong.Id, order).Result();
throw new ArgumentException("Message is neither Pong nor Ping", nameof(message));
}
public static IMessage FromBytes(ByteString bytes)
{
var order = ByteOrder.LittleEndian;
var it = bytes.Iterator();
var b = it.GetByte();
if(b == 1)
return new Ping(it.GetInt(order));
if(b == 2)
return new Pong(it.GetInt(order));
throw new SystemException($"Parse error: expected 1|2 got {b}");
}
In this way you could easily integrate any other serialization library that turns an object into a sequence of bytes.
The other stage that we talked about is a little more involved since reversing a framing protocol means that any received chunk of bytes may correspond to zero or more messages. This is best implemented using a GraphStage (see also Custom processing with GraphStage).
public static ByteString AddLengthHeader(ByteString bytes, ByteOrder order)
=> new ByteStringBuilder().PutInt(bytes.Count, order).Append(bytes).Result();
public class FrameParser : GraphStage<FlowShape<ByteString, ByteString>>
{
private sealed class Logic : GraphStageLogic
{
private readonly FrameParser _parser;
// this holds the received but not yet parsed bytes
private ByteString _stash;
// this holds the current message length or -1 if at a boundary
private int _needed = -1;
public Logic(FrameParser parser) : base(parser.Shape)
{
_parser = parser;
_stash = ByteString.Empty;
SetHandler(parser.Out, onPull: () =>
{
if (IsClosed(parser.In))
Run();
else
Pull(parser.In);
});
SetHandler(parser.In, onPush: () =>
{
var bytes = Grab(parser.In);
_stash += bytes;
Run();
}, onUpstreamFinish: () =>
{
if(_stash.IsEmpty)
CompleteStage();
// wait with completion and let Run() complete when the
// rest of the stash has been sent downstream
});
}
private void Run()
{
if (_needed == -1)
{
// are we at a boundary? then figure out next length
if (_stash.Count < 4)
{
if (IsClosed(_parser.In))
CompleteStage();
else
Pull(_parser.In);
}
else
{
_needed = _stash.Iterator().GetInt(_parser._order);
_stash = _stash.Drop(4);
Run(); // cycle back to possibly already emit the next chunk
}
}
else if (_stash.Count < _needed)
{
// we are in the middle of a message, need more bytes,
// or have to stop if input closed
if (IsClosed(_parser.In))
CompleteStage();
else
Pull(_parser.In);
}
else
{
// we have enough to emit at least one message, so do it
var emit = _stash.Take(_needed);
_stash = _stash.Drop(_needed);
_needed = -1;
Push(_parser.Out, emit);
}
}
}
private readonly ByteOrder _order;
public FrameParser(ByteOrder order)
{
_order = order;
Shape = new FlowShape<ByteString, ByteString>(In, Out);
}
public Inlet<ByteString> In { get; } = new Inlet<ByteString>("FrameParser.in");
public Outlet<ByteString> Out { get; } = new Outlet<ByteString>("FrameParser.out");
public override FlowShape<ByteString, ByteString> Shape { get; }
protected override GraphStageLogic CreateLogic(Attributes inheritedAttributes) => new Logic(this);
}
var framing =
BidiFlow.FromGraph(
GraphDsl.Create(b =>
{
var order = ByteOrder.LittleEndian;
var outbound = b.Add(Flow.Create<ByteString>().Select(bytes => AddLengthHeader(bytes, order)));
var inbound = b.Add(Flow.Create<ByteString>().Via(new FrameParser(order)));
return BidiShape.FromFlows(outbound, inbound);
}));
With these implementations we can build a protocol stack and test it:
/* construct protocol stack
* +------------------------------------+
* | stack |
* | |
* | +-------+ +---------+ |
* ~> O~~o | ~> | o~~O ~>
* Message | | codec | ByteString | framing | | ByteString
* <~ O~~o | <~ | o~~O <~
* | +-------+ +---------+ |
* +------------------------------------+
*/
var stack = codec.Atop(framing);
// test it by plugging it into its own inverse and closing the right end
var pingpong = Flow.Create<IMessage>().Collect(message =>
{
var ping = message as Ping;
return ping != null
? new Pong(ping.Id) as IMessage
: null;
});
var flow = stack.Atop(stack.Reversed()).Join(pingpong);
var result =
Source.From(Enumerable.Range(0, 10))
.Select(i => new Ping(i) as IMessage)
.Via(flow)
.Limit(20)
.RunWith(Sink.Seq<IMessage>(), materializer);
result.Wait(TimeSpan.FromSeconds(1)).Should().BeTrue();
result.Result.ShouldAllBeEquivalentTo(Enumerable.Range(0, 10));
This example demonstrates how BidiFlow subgraphs can be hooked together and also turned around with the .Reversed method. The test simulates both parties of a network communication protocol without actually having to open a network connection—the flows can just be connected directly.
Accessing the Materialized Value Inside the Graph
In certain cases it might be necessary to feed back the materialized value of a Graph (partial, closed or backing a
Source, Sink, Flow or BidiFlow). This is possible by using builder.MaterializedValue which gives an Outlet that
can be used in the graph as an ordinary source or outlet, and which will eventually emit the materialized value.
If the materialized value is needed at more than one place, it is possible to call MaterializedValue any number of
times to acquire the necessary number of outlets.
var aggregateFlow = Flow.FromGraph(GraphDsl.Create(Sink.Aggregate<int, int>(0, (sum, i) => sum + i), (b, aggregate) =>
{
var outlet = b.From(b.MaterializedValue)
.Via(Flow.Create<Task<int>>().SelectAsync(4, x => x))
.Out;
return new FlowShape<int, int>(aggregate.Inlet, outlet);
}));
Be careful not to introduce a cycle where the materialized value actually contributes to the materialized value.
The following example demonstrates a case where the materialized Task of a aggregate is fed back to the aggregate itself.
var cyclicAggregate = Source.FromGraph(GraphDsl.Create(Sink.Aggregate<int, int>(0, (sum, i) => sum + i),
(b, aggregate) =>
{
// - Aggregate cannot complete until its upstream SelectAsync completes
// - SelectAsync cannot complete until the materialized Task produced by
// Aggregate completes
// As a result this Source will never emit anything, and its materialized
// Task will never complete
var flow = Flow.Create<Task<int>>().SelectAsync(4, x => x);
b.From(b.MaterializedValue).Via(flow).To(aggregate);
return new SourceShape<int>(b.From(b.MaterializedValue).Via(flow).Out);
}));
Graph Cycles, Liveness and Deadlocks
Cycles in bounded stream topologies need special considerations to avoid potential deadlocks and other liveness issues. This section shows several examples of problems that can arise from the presence of feedback arcs in stream processing graphs.
The first example demonstrates a graph that contains a naïve cycle. The graph takes elements from the source, prints them, then broadcasts those elements to a consumer (we just used Sink.Ignore for now) and to a feedback arc that is merged back into the main stream via a Merge junction.
Note
The graph DSL allows the connection methods to be reversed, which is particularly handy when writing cycles—as we will see there are cases where this is very helpful.
// WARNING! The graph below deadlocks!
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
var merge = b.Add(new Merge<int>(2));
var broadcast = b.Add(new Broadcast<int>(2));
var print = Flow.Create<int>().Select(s =>
{
Console.WriteLine(s);
return s;
});
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
b.From(source).Via(merge).Via(print).Via(broadcast).To(sink);
b.To(merge).From(broadcast);
return ClosedShape.Instance;
}));
Running this we observe that after a few numbers have been printed, no more elements are logged to the console - all processing stops after some time. After some investigation we observe that:
- through merging from
sourcewe increase the number of elements flowing in the cycle - by broadcasting back to the cycle we do not decrease the number of elements in the cycle
Since Akka Streams (and Reactive Streams in general) guarantee bounded processing (see the "Buffering" section for more
details) it means that only a bounded number of elements are buffered over any time span. Since our cycle gains more and
more elements, eventually all of its internal buffers become full, backpressuring source forever. To be able
to process more elements from source elements would need to leave the cycle somehow.
If we modify our feedback loop by replacing the Merge junction with a MergePreferred we can avoid the deadlock.
MergePreferred is unfair as it always tries to consume from a preferred input port if there are elements available
before trying the other lower priority input ports. Since we feed back through the preferred port it is always guaranteed
that the elements in the cycles can flow.
// WARNING! The graph below stops consuming from "source" after a few steps
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
var merge = b.Add(new MergePreferred<int>(1));
var broadcast = b.Add(new Broadcast<int>(2));
var print = Flow.Create<int>().Select(s =>
{
Console.WriteLine(s);
return s;
});
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
b.From(source).Via(merge).Via(print).Via(broadcast).To(sink);
b.To(merge.Preferred).From(broadcast);
return ClosedShape.Instance;
}));
If we run the example we see that the same sequence of numbers are printed over and over again, but the processing does not stop. Hence, we avoided the deadlock, but source is still back-pressured forever, because buffer space is never recovered: the only action we see is the circulation of a couple of initial elements from source.
Note
What we see here is that in certain cases we need to choose between boundedness and liveness. Our first example would not deadlock if there would be an infinite buffer in the loop, or vice versa, if the elements in the cycle would be balanced (as many elements are removed as many are injected) then there would be no deadlock.
To make our cycle both live (not deadlocking) and fair we can introduce a dropping element on the feedback arc. In this
case we chose the Buffer() operation giving it a dropping strategy OverflowStrategy.DropHead.
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
var merge = b.Add(new Merge<int>(2));
var broadcast = b.Add(new Broadcast<int>(2));
var print = Flow.Create<int>().Select(s =>
{
Console.WriteLine(s);
return s;
});
var buffer = Flow.Create<int>().Buffer(10, OverflowStrategy.DropHead);
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
b.From(source).Via(merge).Via(print).Via(broadcast).To(sink);
b.To(merge).Via(buffer).From(broadcast);
return ClosedShape.Instance;
}));
If we run this example we see that
- The flow of elements does not stop, there are always elements printed
- We see that some of the numbers are printed several times over time (due to the feedback loop) but on average the numbers are increasing in the long term
This example highlights that one solution to avoid deadlocks in the presence of potentially unbalanced cycles
(cycles where the number of circulating elements are unbounded) is to drop elements. An alternative would be to
define a larger buffer with OverflowStrategy.Fail which would fail the stream instead of deadlocking it after
all buffer space has been consumed.
As we discovered in the previous examples, the core problem was the unbalanced nature of the feedback loop. We
circumvented this issue by adding a dropping element, but now we want to build a cycle that is balanced from
the beginning instead. To achieve this we modify our first graph by replacing the Merge junction with a ZipWith.
Since ZipWith takes one element from source and from the feedback arc to inject one element into the cycle,
we maintain the balance of elements.
// WARNING! The graph below never processes any elements
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
var zip = b.Add(ZipWith.Apply<int, int, int>(Keep.Right));
var broadcast = b.Add(new Broadcast<int>(2));
var print = Flow.Create<int>().Select(s =>
{
Console.WriteLine(s);
return s;
});
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
b.From(source).To(zip.In0);
b.From(zip.Out).Via(print).Via(broadcast).To(sink);
b.To(zip.In1).From(broadcast);
return ClosedShape.Instance;
}));
Still, when we try to run the example it turns out that no element is printed at all! After some investigation we realize that:
- In order to get the first element from
sourceinto the cycle we need an already existing element in the cycle - In order to get an initial element in the cycle we need an element from
source
These two conditions are a typical "chicken-and-egg" problem. The solution is to inject an initial
element into the cycle that is independent from source. We do this by using a Concat junction on the backwards
arc that injects a single element using Source.Single.
Warning
We have to add an Async call after creating the instance of Concat. Otherwise Concat will wait upstream to be empty and that will never happen in this case.
RunnableGraph.FromGraph(GraphDsl.Create(b =>
{
var zip = b.Add(ZipWith.Apply<int, int, int>(Keep.Right));
var broadcast = b.Add(new Broadcast<int>(2));
var concat = b.Add(new Concat<int, int>().Async());
var start = Source.Single(0);
var print = Flow.Create<int>().Select(s =>
{
Console.WriteLine(s);
return s;
});
var sink = Sink.Ignore<int>().MapMaterializedValue(_ => NotUsed.Instance);
b.From(source).To(zip.In0);
b.From(zip.Out).Via(print).Via(broadcast).To(sink);
b.To(zip.In1).Via(concat).From(start);
b.To(concat).From(broadcast);
return ClosedShape.Instance;
}));
When we run the above example we see that processing starts and never stops. The important takeaway from this example is that balanced cycles often need an initial "kick-off" element to be injected into the cycle.
 Edit this page
Edit this page